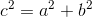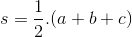Seperti yang telah kita ketahui segitiga merupakan suatu berdiri datar yang dibatasi oleh tiga buah sisi dan mempunyai tiga titik sudut.
Jumlah ketiga titik sudut segitiga yaitu 180°, sehingga apabila besar salah satu atau kedua titik sudutnya diketahui kita dapat mencari besar titik sudut yang lainnya.
Contoh soal:
Perhatikan gambar berikut!
Diketahui ∠A = 45°, ∠B = 60°, tentukan besar sudut C!
180° = ∠A+∠B+∠C
180° = 45°+60°+∠C
∠C = 180° - (45°+60°)
∠C = 180° - 105°
∠C = 75°
Jenis-jenis segitiga:
1. berdasarkan panjang sisinya
2. berdasarkan besar sudutnya
Luas dan Keliling Segitiga
Luas
Luas yaitu 1/2 dikali panjang bantalan dan tingginya.
Keliling
keliling yaitu jumlah panjang sisi-sisi yang membatasi bidang datar tersebut.
Untuk segitiga sama sisi (misalnya panjang sisi-sisinya kita sebut a) luas dan kelilingnya dapat juga kita cari dengan menggunakan rumus;
Contoh soal:
Tentukan luas dan keliling pada segitiga sama kaki berikut, jikalau diketahui PR = 12cm, QS = 8cm, dan QR = 10cm!
Pembahasan:
Pada segitiga diatas PR = bantalan segitiga, dan QS = tingginya.
Keliling = sisi1+sisi2+sisi3 (karena segitiga diatas sama kaki maka PQ = QR = 10cm)
Keliling = 12+10+10
=36 cm
Mencari luas segitiga dengan Teorema Heron
Teorema Heron biasanya digunakan untuk mencari luas segitiga sembarang, misalnya a, b, dan c yaitu ketiga sisi segitiga maka luas segitiga tersebut adalah:
dimana s = semiperimeter yaitu 1/2 keliling, atau
baca juga: Contoh Soal dan Pembahasan Segitiga
Contoh soal:
Diketahui sebuah segitiga sembarang dengan panjang masing-masing sisinya yaitu 5 cm, 7 cm, dan 8 cm. tentukan luas dari segitiga tersebut!
Pembahasan:
hitung nilai semiperimeternya:
Luas segitiga:
Teorema Phytagoras
Teorema Phytagoras yaitu teorema yang menandakan kekerabatan setiap panjang sisi-sisi pada segitiga siku-siku. Teorema ini hanya berlaku untuk segitiga siku-siku, yaitu segitiga yang besar salah satu sudutnya adalah 90°.
Teorema Phytagoras menyatakan bahwa 
dengan titik C sebagai sudut siku-siku.
dengan titik C sebagai sudut siku-siku. Agar lebih terang silakan perhatikan gambar berikut:
Jika ada tiga buah bilangan a, b, dan c yang memenuhi persamaan Phytagoras diatas maka ketiga bilangan tersebut disebut bilangan Triple Phytagoras. (penjelasan lebih lanjut mengenai triple phytagoras silakan baca: Triple Phytagoras)
Contoh soal:
Sebuah segitiga, siku-siku dititik C. Diketahui panjang AB = 25cm, BC = 15cm. Berapakah panjang AC?
Pembahasan:
berdasarkan teorema phytagoras ;
sehingga,
Lingkaran dalam dan Luar Segitiga
Lingkaran dalam segitiga
Lingkaran dalam segitiga yaitu suatu bulat yang berada didalam segitiga serta menyinggung ketiga sisi segitiga tersebut. Jari-jari bulat dalam segitiga dirumuskan sebagai berikut:
dimana r = jari-jari bulat dalam segitiga
L=luas segitiga
s=1/2 keliling segitiga
Lingkaran luar segitiga
Lingkaran luar segitiga yaitu bulat yang berada diluar sigitiga serta keliling segitiga tersebut menyinggung perpotongan tiga garis segitiga. Jari-jari bulat luar segitiga dirumuskan sebagai berikut:
Lingkaran luar segitiga yaitu bulat yang berada diluar sigitiga serta keliling segitiga tersebut menyinggung perpotongan tiga garis segitiga. Jari-jari bulat luar segitiga dirumuskan sebagai berikut:
R = jari-jari bulat luar segitiga
a, b, dan c = 3 sisi segitiga
L = luas segitiga
L = luas segitiga
Perhatikan rumus bulat dalam maupun bulat luar segitiga diatas, masing-masing terdapat L (Luas segitiga), luas segitiga disini dapat kita cari dengan mengetahui jenis segitiga yang ada pada bulat dalam maupun bulat luar segitiga tersebut. (penjelasan lebih lanjut mengenai bulat dalam dan bulat luar segitiga akan saya buat pada artikel selanjutnya).
Contoh soal:
Tentukan jari-jari bulat dalam segitiga berikut ini jikalau diketahui panjang AB = 16cm, BC = 12cm, dan AC = 20cm!
Pembahasan:
kemudian hitung luas segitiga:
sehingga nilai jari-jarinya adalah:
Demikian postingan mengenai Rumus Segitiga Lengkap Beserta Contoh Soalnya. Untuk latihan soalnya silakan lihat di Kumpulan Soal Segitiga. Semoga bermanfaat.
Mohon maaf jikalau ada kata ataupun perhitungan yang salah dalam postingan diatas.